A bead of radius R is falling through a fluid under the influence of gravity. We want to establish a relationship between the bead’s characteristics (its size and density), the fluid’s characteristics (its density and viscosity) and the terminal velocity of the bead.
The begin with, we write down the forces acting on the bead:
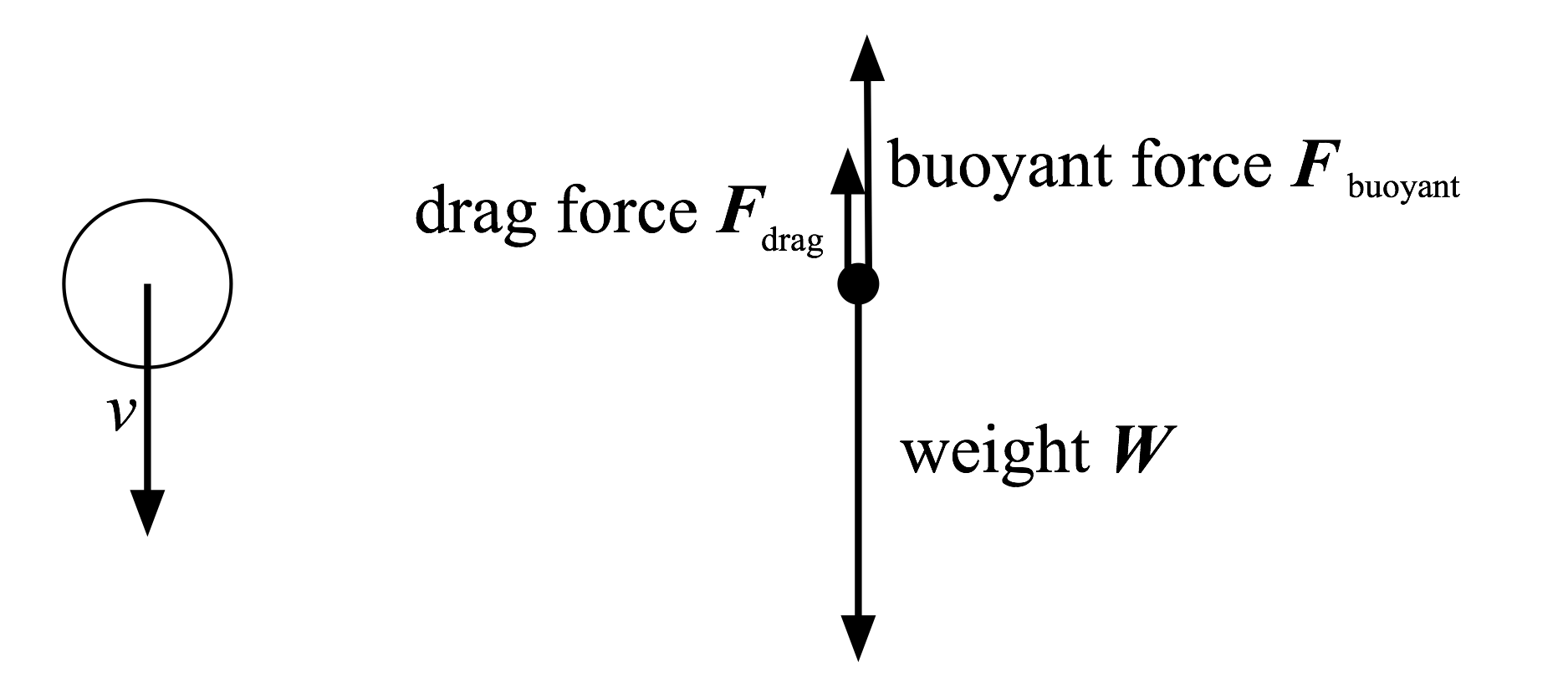
The weight and buoyant force are given by:
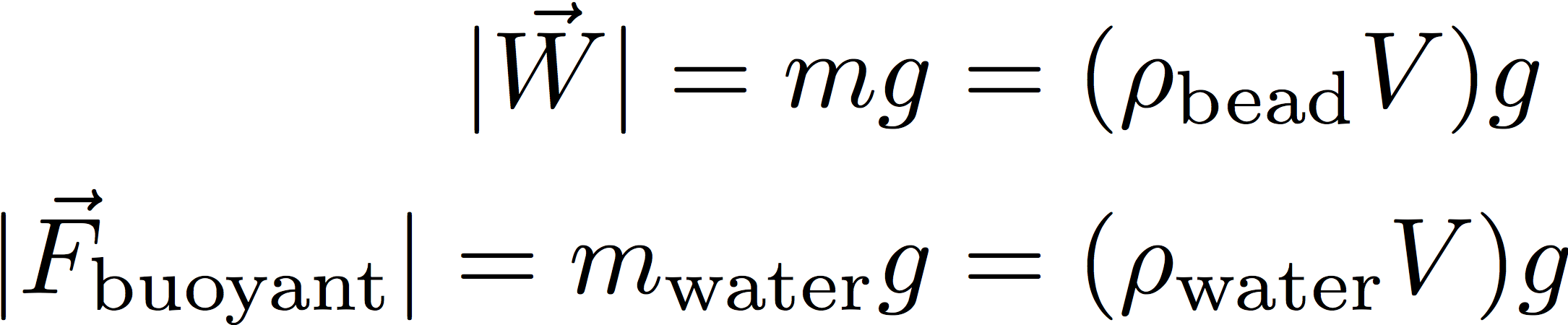
where the ρ‘s are densities (in kg/m3), V is the bead’s volume, and g is the acceleration due to gravity (9.81 m/s2). You may not have seen the buoyant force written down this way, but we all know that when you submerge something in water its effective weight goes down; if the object is denser than water it will still sink (net force downward) but if it is less dense than water it will float (net force upward). This emerges naturally from the effective weight of the submerged bead:
![]()
There are two commonly used expressions for the drag force.
We are trying to determine which of these expressions most accurately describes the behavior of the beads in our experimental situation.
Since our beads are denser than water, if a bead starts from rest it will accelerate downwards. As it picks up speed, the drag force (which opposes motion, and is therefore upward) will increase until it completely cancels the effective weight. At that point, the net force on the bead is zero so the bead’s velocity becomes constant; this is called the terminal velocity. Mathematically, terminal velocity is defined as the velocity at which ![]() Keep in mind that the drag force depends on the velocity v.
Keep in mind that the drag force depends on the velocity v.
